0%

第12章使用FP-growth算法来高效发现频繁项集

发表于 2020-06-03 分类于机器学习阅读次数： 2.6k 2 分钟

前言

在第11章时我们已经介绍了用 Apriori 算法发现 频繁项集 与 关联规则。
本章将继续关注发现 频繁项集 这一任务，并使用 FP-growth 算法更有效的挖掘 频繁项集。

FP-growth 算法简介

一种非常好的发现频繁项集算法。
基于Apriori算法构建,但是数据结构不同，使用叫做 FP树 的数据结构结构来存储集合。下面我们会介绍这种数据结构。

FP-growth 算法步骤

基于数据构建FP树
从FP树种挖掘频繁项集

FP树介绍

FP树的节点结构如下:

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue     # 节点名称
        self.count = numOccur     # 节点出现次数
        self.nodeLink = None      # 不同项集的相同项通过nodeLink连接在一起
        # needs to be updated
        self.parent = parentNode  # 指向父节点
        self.children = {}        # 存储叶子节点
```   
         
## FP-growth 原理
基于数据构建FP树

步骤1:
   1. 遍历所有的数据集合，计算所有项的支持度。
   2. 丢弃非频繁的项。
   3. 基于 支持度 降序排序所有的项。
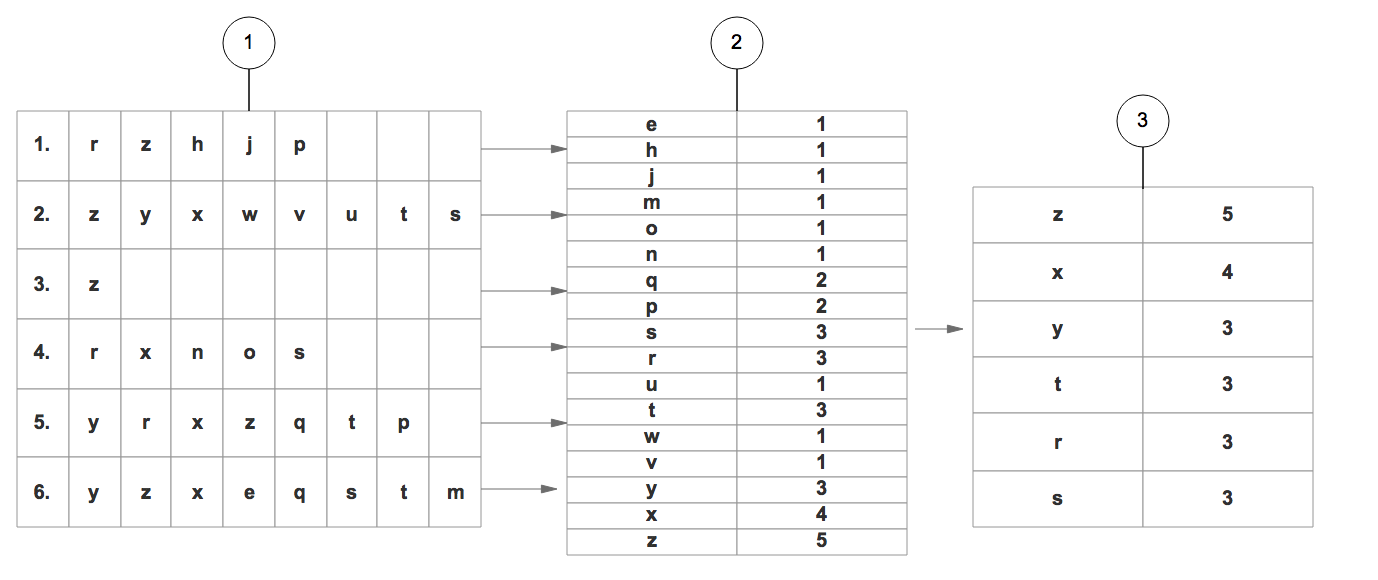
   ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤1-3.png)
   4. 所有数据集合按照得到的顺序重新整理。
   5. 重新整理完成后，丢弃每个集合末尾非频繁的项。
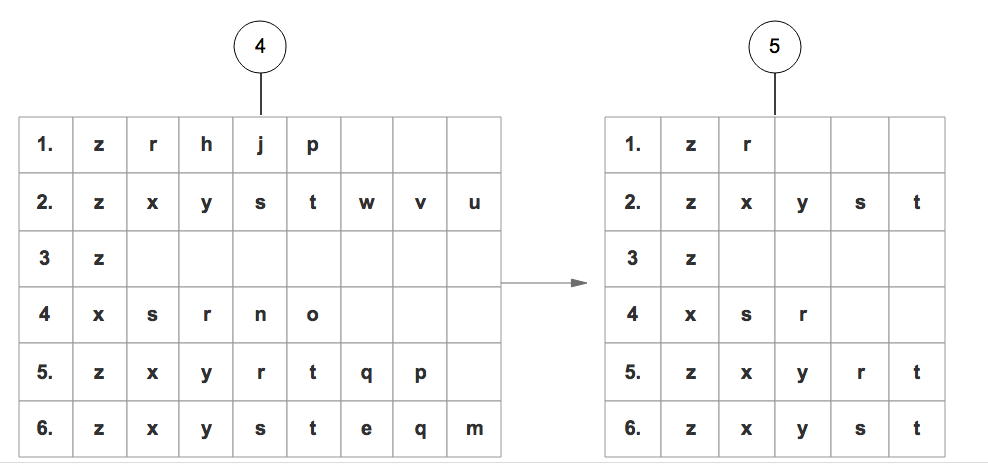
   ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤4-5.png)

步骤2:
   6. 读取每个集合插入FP树中，同时用一个头部链表数据结构维护不同集合的相同项。  
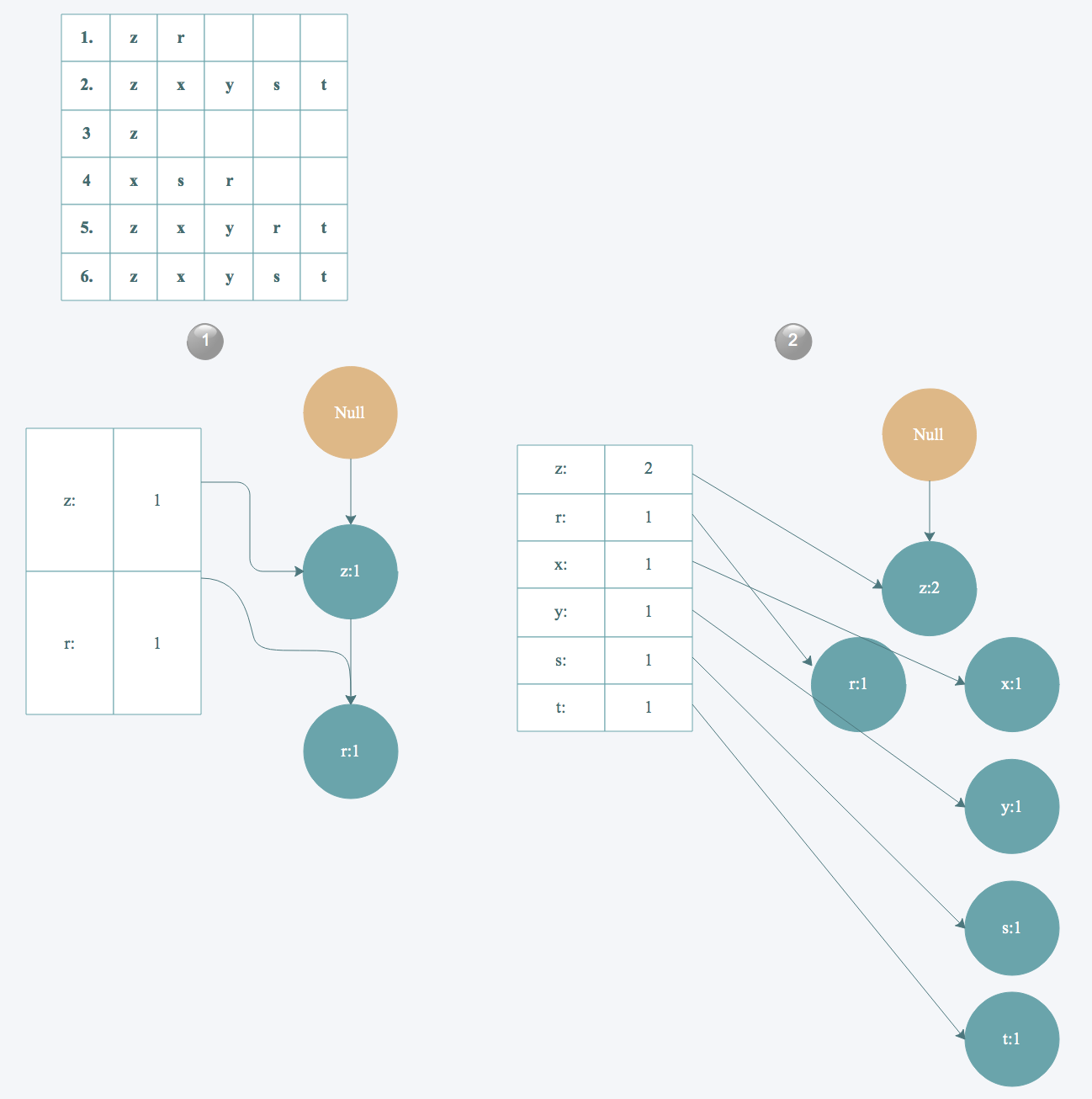
   ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤6-1.png)
   最终得到下面这样一棵FP树
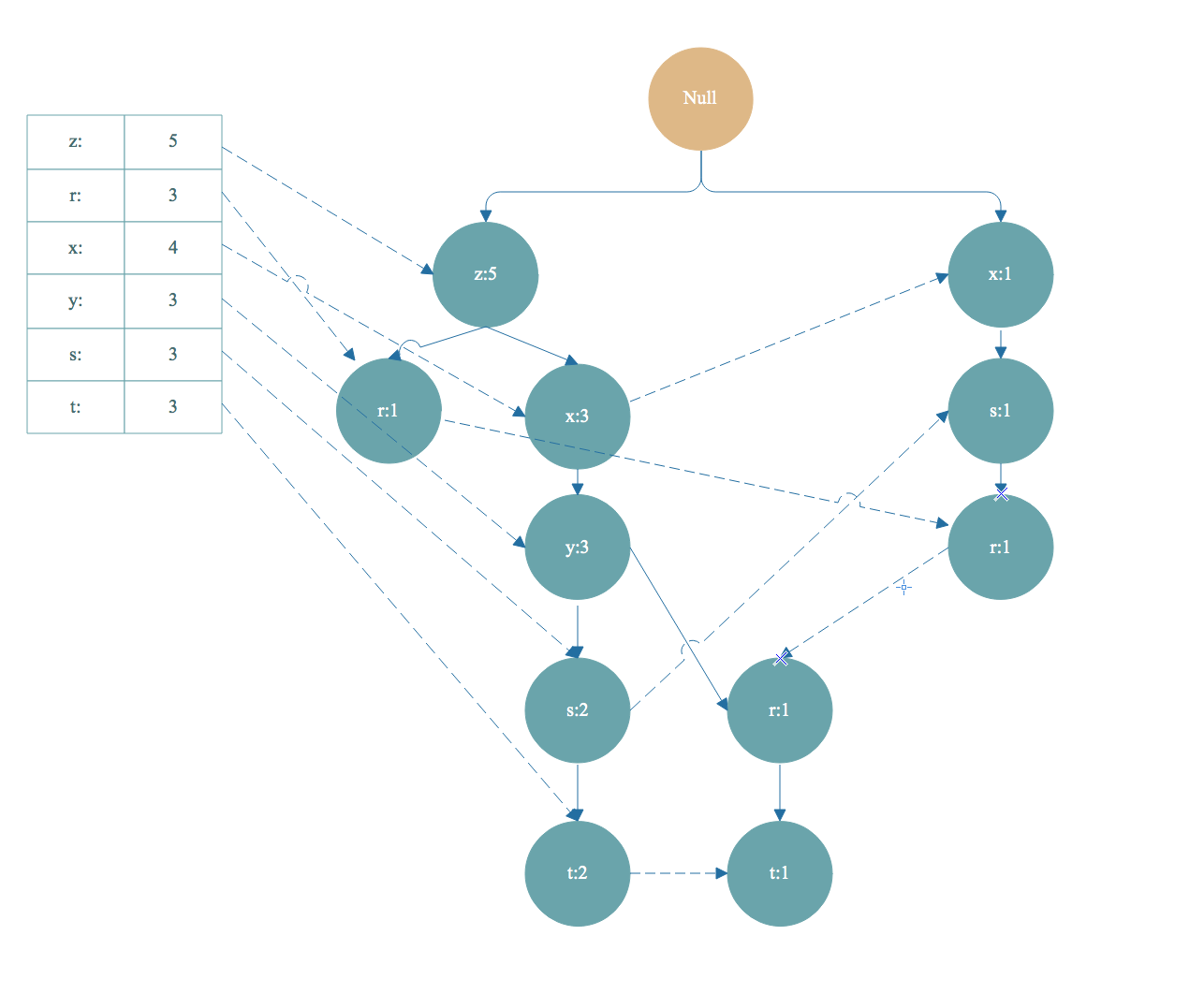
   ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤6-2.png)


从FP树中挖掘出频繁项集

步骤3:
   1. 对头部链表进行降序排序
   2. 对头部链表节点从小到大遍历，得到条件模式基，同时获得一个频繁项集。
        ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤6-2.png)
        如上图，从头部链表 t 节点开始遍历，t 节点加入到频繁项集。找到以 t 节点为结尾的路径如下:
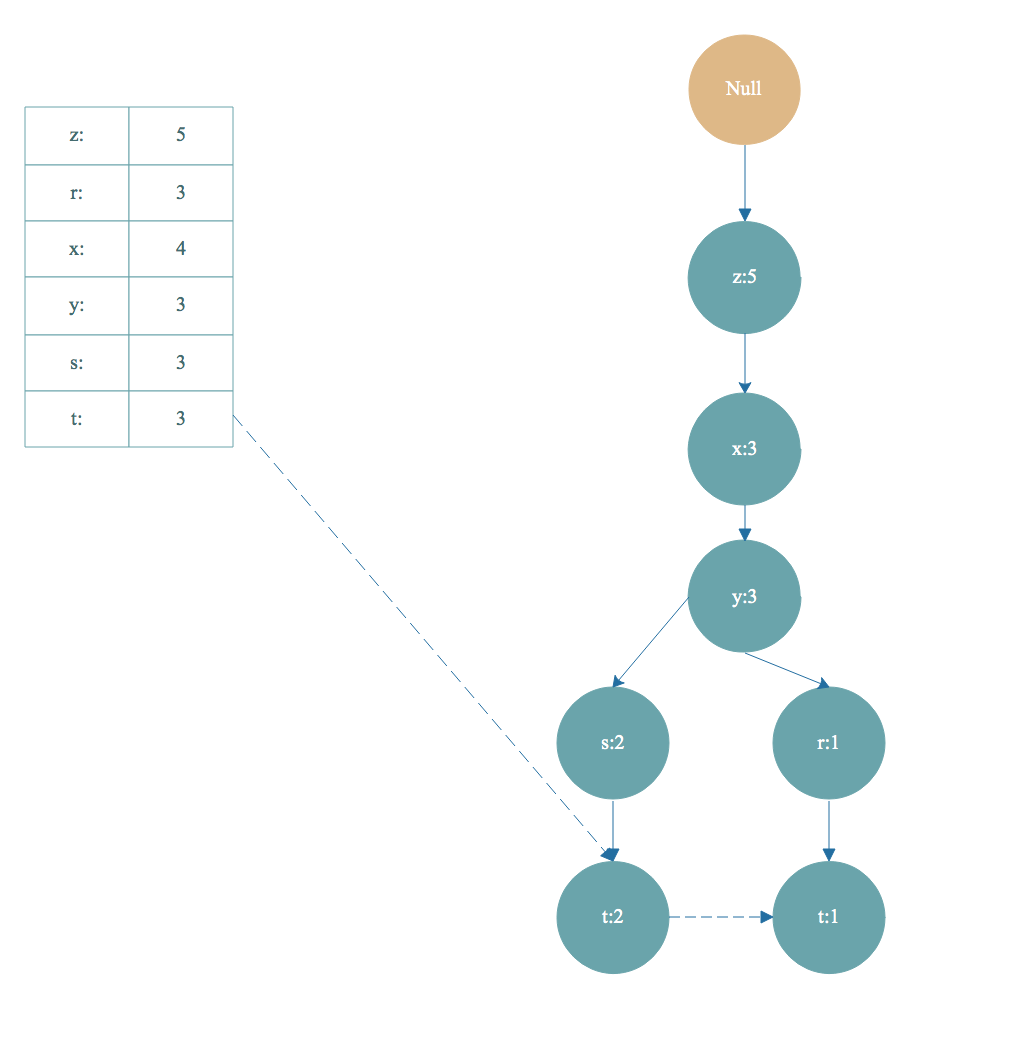
        ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤7-1.png)
        去掉FP树中的t节点，得到条件模式基<左边路径, 右边是值>[z,x,y,s,t]:2，[z,x,y,r,t]:1 。条件模式基的值取决于末尾节点 t ，因为 t 的出现次数最小，一个频繁项集的支持度由支持度最小的项决定。所以 t 节点的条件模式基的值可以理解为对于以 t 节点为末尾的前缀路径出现次数。
       
   3. 条件模式基继续构造条件 FP树， 得到频繁项集，和之前的频繁项组合起来，这是一个递归遍历头部链表生成FP树的过程，递归截止条件是生成的FP树的头部链表为空。
        根据步骤 2 得到的条件模式基 [z,x,y,s,t]:2，[z,x,y,r,t]:1 作为数据集继续构造出一棵FP树，计算支持度，去除非频繁项，集合按照支持度降序排序，重复上面构造FP树的步骤。最后得到下面 t-条件FP树 :
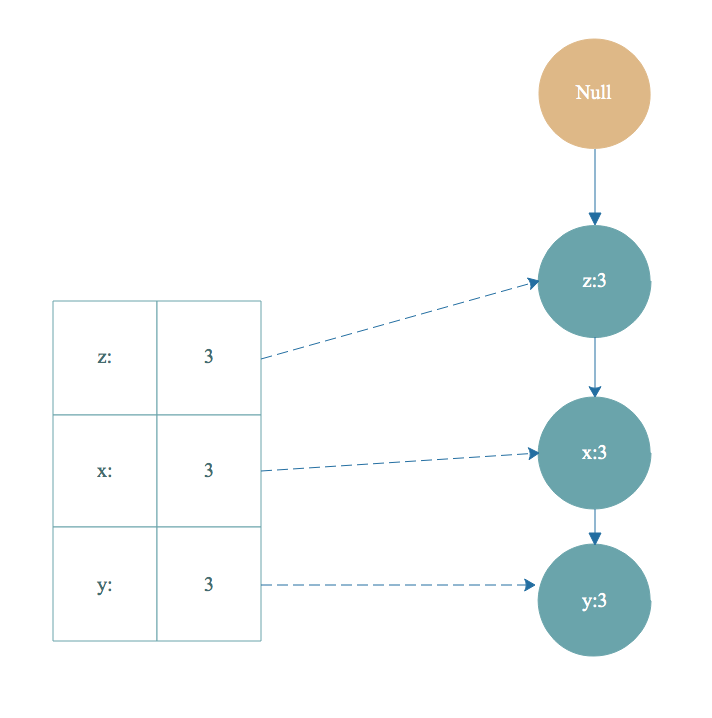
        ![](http://data.apachecn.org/img/AiLearning/ml/12.FP-growth/步骤7-2.png)
        然后根据 t-条件FP树 的头部链表进行遍历，从 y 开始。得到频繁项集 ty 。然后又得到 y 的条件模式基，构造出 ty的条件FP树，即 ty-条件FP树。继续遍历ty-条件FP树的头部链表，得到频繁项集 tyx，然后又得到频繁项集 tyxz. 然后得到构造tyxz-条件FP树的头部链表是空的，终止遍历。我们得到的频繁项集有 t->ty->tyz->tyzx，这只是一小部分。
   * 条件模式基:头部链表中的某一点的前缀路径组合就是条件模式基，条件模式基的值取决于末尾节点的值。
   * 条件FP树:以条件模式基为数据集构造的FP树叫做条件FP树。

FP-growth 算法优缺点:

优点： 1. 因为 FP-growth 算法只需要对数据集遍历两次，所以速度更快。

2. FP树将集合按照支持度降序排序，不同路径如果有相同前缀路径共用存储空间，使得数据得到了压缩。
3. 不需要生成候选集。
4. 比Apriori更快。

缺点： 1. FP-Tree第二次遍历会存储很多中间过程的值，会占用很多内存。
```
2. 构建FP-Tree是比较昂贵的。
```
适用数据类型：标称型数据(离散型数据)。

FP-growth 代码讲解

完整代码地址: https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/12.FrequentPattemTree/fpGrowth.py

main 方法大致步骤:

if __name__ == "__main__":
    simpDat = loadSimpDat()                       #加载数据集。
    initSet = createInitSet(simpDat)              #对数据集进行整理，相同集合进行合并。
    myFPtree, myHeaderTab = createTree(initSet, 3)#创建FP树。
    freqItemList = []
    mineTree(myFPtree, myHeaderTab, 3, set([]), freqItemList) #递归的从FP树中挖掘出频繁项集。
    print freqItemList

大家看懂原理，再仔细跟踪一下代码。基本就没有问题了。

本文转载于 ApacheCN
GitHub地址: https://github.com/apachecn/AiLearning